以前看到四边形不等式或叫决策单调性优化 dp,看到绕来绕去的式子和繁琐的证明总是望而却步。
数理基础简单打一下后再来看时发现,其实模型并不复杂,证明大多较为基础,故记此文加以巩固。
部分证明过程会以 Markdown 中引用的格式进行标注,笔者学艺不精还请指出错误及不足之处。
代码大部分是自己口胡出来的,可能写得乱了点。
四边形不等式
设函数 $w(x,y)$,其中 $x,y$ 整数,若对于任意整数 $a,b,c,d$,满足 $a\leq b\leq c\leq d$,都有 $w(a,c)+w(b,d)\leq w(a,d)+w(b,c)$ 成立,则称 $w$ 满足四边形不等式。
简记为:交叉小于等于包含。
定理一
若对于任意正整数 $a,b$,满足 $a<b$ ,都有 $w(a,b)+w(a+1,b+1)\leq w(a,b+1)+w(a+1,b)$ 成立,则 $w$ 满足四边形不等式。
我的记法是两步一起蹦跶 ($(a,b)\to(a+1,b+1)$)不如一步一步走远 ($(a,b+1),a(a+1,b)$),有点像绕口令的感觉了wwwww。
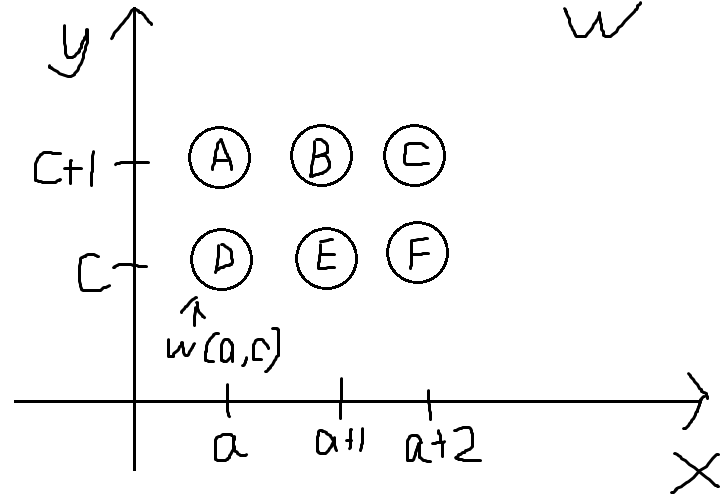
当 $a+1<c$ 时,由条件得 $C+B\leq A+D,D+E\leq B+F$,两式相加化简可得 $C+E\leq A+F$,以此类推,对于 $a\leq b\leq c$ 都有 $w(a,c)+w(b,c+1)\leq w(a,c+1)+w(b,c)$ 成立。
同理,对于所有 $a\leq b\leq c\leq d$,都有 $w(a,c)+w(b,d)\leq w(a,d)+w(b,c)$ 成立。
1D1D 问题的优化
决策单调性:设 $p_i$ 为 $f_i$ 最优转移的位置(决策点),$p$ 单调不降即为具有决策单调性。
一般地,对于 $f_i=\min\{g_j+w(j,i)\}$ 的状态转移方程,若 $w$ 满足四边形不等式,则 $f$ 满足决策单调性。
值得注意的是,这里的 $g_j$ 是指的关于 $j$ 的函数,其有可能包括 dp 的 $f_j$,也有可能仅包括与 $f_j$ 无关的其他 $a_j,b_j,c_j…$ 其他关于 $j$ 的值,也有可能为常数,但不影响结论的正确性。$\min$ 还是 $\max$ 也不影响。
已知 $g_{p_i}+w(p_i,i)\leq g_j+w(j,i),j<p_i$ 以及 $w$ 满足四边形不等式。
求证 $p_{i’}\geq p_i,i’>i$。
为了体现想出这个证明的思路,以下的过程表述并不严谨。
$p_{i’}\geq p_i$ 等价于 $g_{p_i}+w(p_i,i’)\leq g_j+w(j,i’),j<p_i$。
那么就是想办法把已知条件 $g_{p_i}+w(p_i,i)\leq g_j+w(j,i),j<p_i$ 中的 $w(p_i,i)$ 换成 $w(p_i,i’)$,$w(j,i)$ 换成$w(j,i’)$。
由于 $w$ 满足四边形不等式且 $j<p_i<i<i’$,
所以 $w(j,i)+w(p_i,i’)\leq w(p_i,i)+w(j,i’)$。
移项得 $w(p_i,i’)-w(p_i,i)\leq w(j,i’)-w(j,i)$。
与已知中的不等式相加得到 $g_{p_i}+w(p_i,i)\leq g_j+w(j,i),j<p_i$。
故 $p_{i’}\geq p$。
单调队列 + 二分
考虑维护 $p$ 数组,初始全为 $0$,从前往后计算完 $f_i$ 时,$f_i$ 会更新一个后缀的 $p$。
暴力做这个东西非常完蛋,考虑将 $p$ 的一段段连续区间看成一个拿下来放到一个单调栈里,二分单调栈的位置,使得前半部分用 $i$ 转移不比之前的 $p$ 优,后半部分用 $i$ 转移比之前的 $p$ 更优,如果需要断开就断开,然后把后缀的都弹出来,压入新的这个后缀。
当然,dp 到 $i$ 时 $<i$ 的 $p$ 是不需要的,所以可以把单调栈改成单调队列。
每次最多只会压入一个点代表的区间,均摊下来,加上二分,时间复杂度是 $\mathcal{O}(n\log n)$ 的。
栗题一:Luogu P3515 [POI2011]Lightning Conductor
$a_j\leq a_i+p_i-\sqrt{|i-j|}$ 等价于 $p_i\geq a_j-a_i+\sqrt{|i-j|}$。求最小的 $p_i$ 使得这个柿子成立,所以 $p_i=\max\{a_j-a_i+\sqrt{|i-j|}\}$,先钦定 $i>j$,$i<j$ 时反过来再做一遍就行。
把 $a_i$ 从 $\max$ 中提出来,把 $a_j$ 看成上文中的 $g_j$,也就是关于 $j$ 的函数。
由于 dp 中为 $\max$,所以需证明 $w(j,i)=-\sqrt{i-j}$ 满足四边形不等式,即可证明 $p$ 的决策单调性,便可以决策单调性优化。
求证:$w(l,r)=-\sqrt{r-l}$ 满足四边形不等式,即对于任意 $a<b$ 均满足 $w(a,b)+w(a+1,b+1)\leq w(a,b+1)+w(a+1,b)$ 即可。
注意到 $f(x)=\sqrt{x}$ 是上凸的,所以由琴生不等式结论得证。
化简到这里,打个表也易知 $2\sqrt{x}\geq \sqrt{x+1}+\sqrt{x-1}$ 成立。
综上所述,$w$ 满足四边形不等式。
实现上要注意用 double 来比较,根号不上取整而是直接开。
因为如果转移点 $j,k$ 根号都上取整,在算答案的 $i$ 小时大小可能会一样,$i$ 变大的时候大小会发生变化。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
| #include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm>
typedef long long ll;
typedef double ld;
template <typename T> T Max(T x, T y) { return x > y ? x : y; }
template <typename T> T Min(T x, T y) { return x < y ? x : y; }
template <typename T> T Abs(T x) { return x < 0 ? -x : x; }
template <typename T>
T& read(T& r) {
r = 0; bool w = 0; char ch = getchar();
while(ch < '0' || ch > '9') w = ch == '-' ? 1 : 0, ch = getchar();
while(ch >= '0' && ch <= '9') r = r * 10 + (ch ^ 48), ch = getchar();
return r = w ? -r : r;
}
const int N = 500010;
int n, a[N], qh, qt;
ll f[N];
struct Node {
int l, r, p;
Node(int ll = 0, int rr = 0, int pp = 0) { l = ll; r = rr; p = pp; }
}q[N];
ld w(int x, int y) {
return a[x] - a[y] + std::sqrt(y-x);
}
void solve(int op) {
for(int i = 1; i <= n; ++i) q[i] = Node();
q[qh = qt = 1] = Node(1, n, 1);
for(int i = 1; i <= n; ++i) {
while(qh < qt && q[qh].r < i) ++qh;
if(!op) f[i] = Max(f[i], (ll)std::ceil(w(q[qh].p, i)));
else f[n-i+1] = Max(f[n-i+1], (ll)std::ceil(w(q[qh].p, i)));
if(q[qh].l == q[qh].r) ++qh;
else q[qh].l = i+1;
while(qh <= qt && w(q[qt].p, q[qt].l) < w(i, q[qt].l)) --qt, q[qt].r = q[qt+1].r;
if(qh > qt) q[++qt] = Node(i+1, n, i);
else {
int l = q[qt].l, r = q[qt].r, mid, t = 0;
while(l <= r) {
mid = (l + r) >> 1;
if(w(q[qt].p, mid) < w(i, mid)) t = mid, r = mid-1;
else l = mid+1;
}
if(t) {
if(t == q[qt].l) q[qt].p = i;
else ++qt, q[qt] = Node(t, q[qt-1].r, i), q[qt-1].r = t-1;
}
}
}
}
signed main() {
read(n);
for(int i = 1; i <= n; ++i) read(a[i]);
solve(0);
std::reverse(a + 1, a + n + 1);
solve(1);
for(int i = 1; i <= n; ++i) printf("%lld\n", f[i]);
return 0;
}
|
栗题二:[NOI2009] 诗人小G
设 $f_i$ 为考虑前 $i$ 个单词的最小代价,枚举 $j$,让 $(j,i]$ 的单词分在同一行中。设 $a$ 的前缀和为 $s$,可得:
为简化计算,将 $a_i,L$ 都 $+1$,得
设 $w(l,r)=|s_r-s_l-L|^p$,证明 $w$ 满足四边形不等式则可以决策单调性优化。
求证:对于任意 $a<b$ 均满足 $w(a,b)+w(a+1,b+1)\leq w(a,b+1)+w(a+1,b)$ 即可。
由于 $s_{a+1}>s_a$,设函数 $f(x)=|x|^p-|x-c|^p$,其中 $c$ 为 $>0$ 的常数,证明其单调不升即可。
分类讨论一下:
假如 $p$ 为奇数,并且 $x\in [-\infty,0]$:
化简一下 $f$:$f(x)=-x^p+(x-c)^p$。
求导得 $f’(x)=-px^{p-1}+(p-1)\cdot (x-c)^{p-1}\leq 0$,所以此时 $f$ 单调不升。
其余情况类似,不多赘述,均为化简 $f$ 后证明 $f’(x)\leq 0$ 即可。
如此,我们证明了 $w$ 满足四边形不等式,故可以决策单调性优化。
方法就是前面讲过的单调队列 + 二分。注意答案可能很大,开 long double。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
| #include<iostream>
#include<cstdio>
#include<vector>
#include<algorithm>
#include<cstring>
typedef long double ll;
template <typename T> T Max(T x, T y) { return x > y ? x : y; }
template <typename T> T Min(T x, T y) { return x < y ? x : y; }
template <typename T> T Abs(T x) { return x < 0 ? -x : x; }
template <typename T>
T& read(T& r) {
r = 0; bool w = 0; char ch = getchar();
while(ch < '0' || ch > '9') w = ch == '-' ? 1 : 0, ch = getchar();
while(ch >= '0' && ch <= '9') r = r * 10 + (ch ^ 48), ch = getchar();
return r = w ? -r : r;
}
ll qpow(ll x, int y) {
ll sumq = 1;
while(y) {
if(y & 1) sumq = sumq * x;
x = x * x;
y >>= 1;
}
return sumq;
}
const int N = 100010;
int n, L, P, p[N], a[N], s[N];
int qh, qt;
struct Node {
int p, l, r;
Node(int pp = 0, int ll = 0, int rr = 0) { p = pp; l = ll; r = rr; }
}q[N];
char ch[N][31];
ll f[N];
ll w(int j, int i) {
return f[j] + qpow(Abs(s[i] - s[j] - L), P);
}
void print(int x) {
if(!x) return ;
print(p[x]);
for(int i = p[x]+1; i <= x; ++i) {
printf("%s", ch[i]+1);
if(i < x) putchar(' ');
}
puts("");
}
void solve() {
read(n); read(L); read(P); ++L;
for(int i = 1; i <= n; ++i) {
scanf("%s", ch[i]+1);
a[i] = std::strlen(ch[i]+1);
p[i] = q[i].p = q[i].l = q[i].r = 0;
s[i] = s[i-1] + a[i] + 1;
}
qh = 1; qt = 1;
q[1] = Node(0, 1, n);
for(int i = 1; i <= n; ++i) {
while(qh < qt && q[qh].r < i) ++qh;
f[i] = w(q[qh].p, i); p[i] = q[qh].p;
if(q[qh].l == q[qh].r) ++qh;
else ++q[qh].l;
while(qh <= qt && w(q[qt].p, q[qt].l) > w(i, q[qt].l)) --qt, q[qt].r = q[qt+1].r;
if(qh > qt) q[++qt] = Node(i, i+1, n);
else {
int l = q[qt].l, r = q[qt].r, mid = 0, t = 0;
while(l <= r) {
mid = (l + r) >> 1;
if(w(q[qt].p, mid) > w(i, mid)) t = mid, r = mid-1;
else l = mid+1;
}
if(t) {
if(t == q[qt].l) q[qt].p = i;
else ++qt, q[qt] = Node(i, t, q[qt-1].r), q[qt-1].r = t-1;
}
}
}
if(f[n] > 1000000000000000000ll) {
puts("Too hard to arrange");
return ;
}
printf("%lld\n", (long long)f[n]);
print(n);
}
signed main() {
int T; read(T);
while(T--) {
solve();
puts("--------------------");
}
return 0;
}
|
分治
单调队列+二分的方法可以解决大多数的决策单调性优化问题。对于更特殊的情况,决策点和决策点如果是互相独立的,那么可以采用分治解决。适用性没有单调队列+二分更强,但是也可能拿来解决某些问题。
大致的思路是:定义 solve(l,r,L,R) 为求解 $[L,R]$ 的状态值,已知这些状态的最优决策点在 $[l,r]$ 中,每次暴力求出 $mid=[\frac{L+R}{2}]$ 处的状态值,从最优决策点断开分治解决。
由于每一层递归下去状态数 $len=R-L+1$ 都会折半,所以递归树的层数是 $\mathcal{O}(\log n)$ 级别,递归树每层 solve 的总复杂度是决策点总数即 $\mathcal{O}(n)$,所以总的时间复杂度是 $\mathcal{O}(n\log n)$.
栗题三:Codeforces 868F Yet Another Minimization Problem
考虑 $f_{i,j}$ 代表前 $i$ 个数分成 $j$ 段,然后有个决策单调性优化,但是这个一段区间的代价 $w(l,r)$ 比较难算,如果单独看这个东西是小 Z 的袜子,可以归约到 $O(\sqrt n)\times O(\sqrt n)$ 的矩阵乘法,看上去很完蛋。
但注意到如果选择分治来算这个决策单调性,$w$ 用类似莫队的东西暴力移动两个指针,由于分治最多有 $\log n$ 层,每层的移动次数是 $\mathcal{O}(n)$ 的,所以这个 $w$ 的统计次数是 $\mathcal{O}(n\log n)$ 的,总复杂度就是 $\mathcal{O}(kn\log n)$.
斜率优化
有一部分决策单调性问题实际上就是斜率优化的一种,具体的原理就不多谈啦其实就是懒。
一点总结
其实大部分的题要点还是能看出来这个满足决策单调性,有时候证不出来也可以打个表看看有没有单调性。
至于栗题的话,如果提前告诉你这个题决策点是单调了从而决策单调性优化,那就没什么意义了,所以就不放啦其实就是懒。
